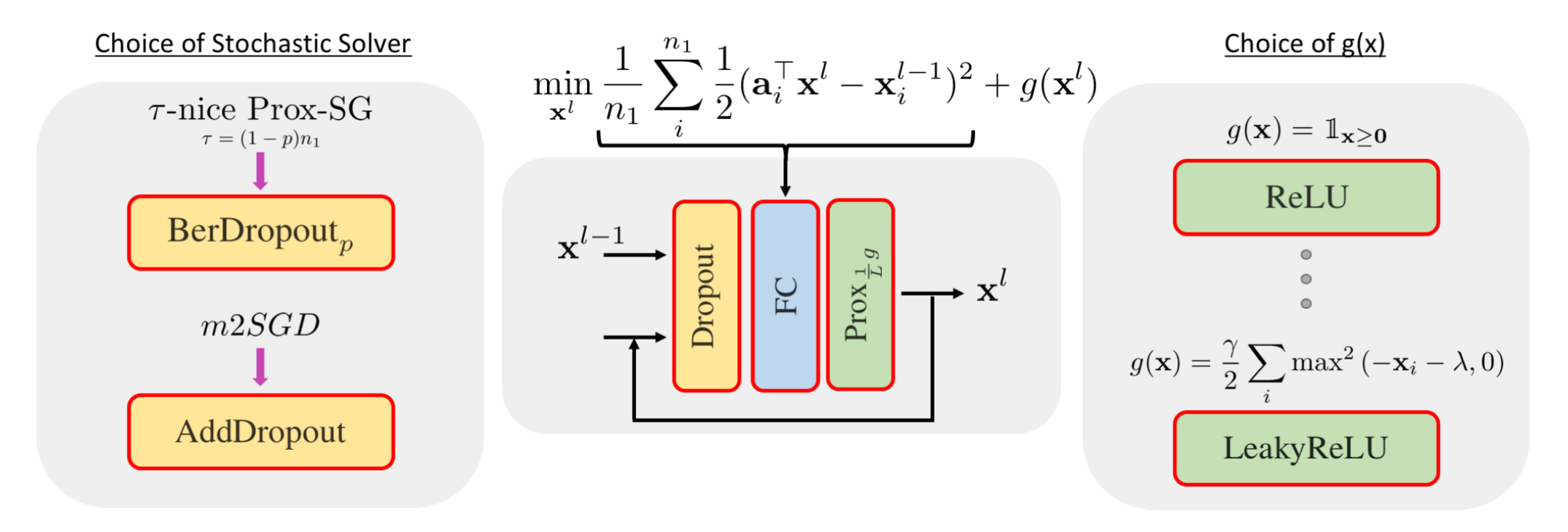
We provide a novel perspective on the forward pass through a block of layers in a deep network. In particular, we show that a forward pass through a standard dropout layer followed by a linear layer and a non-linear activation is equivalent to optimizing a convex objective with a single iteration of a \tau-nice Proximal Stochastic Gradient method. We further show that replacing standard Bernoulli dropout with additive dropout is equivalent to optimizing the same convex objective with a variance-reduced proximal method. By expressing both fully-connected and convolutional layers as special cases of a high-order tensor product, we unify the underlying convex optimization problem in the tensor setting and derive a formula for the Lipschitz constant L used to determine the optimal step size of the above proximal methods. We conduct experiments with standard convolutional networks applied to the CIFAR-10 and CIFAR-100 datasets and show that replacing a block of layers with multiple iterations of the corresponding solver, with step size set via L, consistently improves classification accuracy.
Deep Layers as Stochastic Solvers